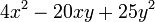domingo, 3 de junio de 2012

función matemática


¿que es una función?

En matemática, una función (f) es una relación entre un conjunto dado X (llamado dominio) y otro conjunto de elementos Y (llamado codominio) de forma que a cada elemento x del dominio le corresponde un único elemento f(x) del codominio (los que forman el recorrido, también llamado rango o ámbito).

Dominio y rango de una función
Como ya vimos, el dominio de una función es el conjunto de valores para los cuales la función está definida; es decir,  son todos los valores que puede tomar la variable independiente (la x).
Por ejemplo la función f(x) = 3x2 – 5x está definida para todo número real (x puede ser cualquier número real). Así el dominio de esta función es el conjunto de todos los números reales.
En cambio, la función    tiene como dominio todos los valores de x para los cuales −1< x < 2, porque aunque pueda tomar cualquier valor real diferente de –2, en su definición determina en qué intervalo está comprendida.
Si el dominio no se específica, debe entenderse que el dominio incluye a todos los números reales para los cuales la función tiene sentido.
En el caso de la función   , el dominio de esta función son todos los números reales mayores o iguales a –3, ya que  x + 3 debe ser mayor o igual que cero para que exista la raíz cuadrada.
Como resumen, para determinar el dominio de una función, debemos considerar lo siguiente:
Si la función tiene radicales de índice par, el dominio está conformado por todos los números reales para los cuales la cantidad sub-radical sea mayor o igual a cero.
Si la función es un polinomio; una  función  de  la  forma   f(x) = a0 + a1x + a2x2 +...+ anxn (donde a0, a1, a2,..., an son constantes y numero entero no negativo), el dominio está conformado por el conjunto de todos los números reales.
Si la función es racional; esto es, si es el cociente de dos polinomios, el dominio está conformado por todos los números reales para los cuales el denominador sea diferente de cero.
El rango (recorrido o ámbito) es el conjunto formado por todas las imágenes; es decir, es el conjunto conformado por todos los valores que puede tomar la variable dependiente; estos valores están determinados además, por el dominio de la función.
Ejemplo
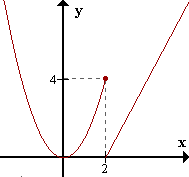
Identificar dominio y rango de la función   
Veamos:
Como la función tiene radicales el dominio está conformado por todos los valores para los cuales  x – 2 ≥ 0. Esto es, el dominio de la función incluye todos los reales que son mayores o iguales a 2.
El rango es igual al conjunto de los números reales positivos incluyendo el cero; puesto que al reemplazar los valores del dominio se obtienen únicamente valores positivos bajo la función f.



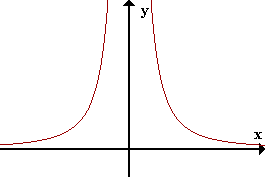
limite de una función
El límite de una función es un concepto fundamental del cálculo diferencial matemático, un caso de límite aplicado a las funciones.
Informalmente, el hecho que una función f tiene un límite L en el punto c, significa que el valor de f puede ser tan cercano a L como se desee, tomando puntos suficientemente cercanos a c, independientemente de lo que ocurra en c.







derivada de una función


Una función es derivable en un conjunto si es derivable en todos los puntos de dicho conjunto.

Si una función (f,D) es derivable en un subconjunto D´ de su dominio D, es posible definir una nueva función que asocia a cada número real de D´ la derivada de fen ese punto:
La función así definida se llama función derivada o, simplemente, derivada de f. Se nota por f´ o también por Df(x).

De la misma forma, a partir de la derivada primera se puede definir, si existe, su derivada, y que recibe el nombre de derivada segunda:
Y así sucesivamente las demás.





continuidad de una función

Una función f(x) es continua en un punto a si limx->af(x) = f(a).
Nota: observar que debe existir f(a) y debe existir el limx->a f(x) y debe ser igual a f(a).
Ejemplos de discontinuidad



f(x)= 1/x2
Discontinua en x=0 (No existe f(0))










f(x) = x2 si x <= 2
        2x - 4 si x > 2 

Discontinua en x=2.

Si bien existe f(2), no existe limx->2f(x), pueslimx->2-f(x)=4 y limx->2+f(x)=0



Sin embargo, si miramos la función para x próximos a 2 pero menores, e ignoramos los x mayores que 2, la función es continua en 2 "por la izquierda".


máximos y mínimos







Publicado por en No hay comentarios:

sábado, 2 de junio de 2012

casos de factorizacion

Caso I - Factor común


¿Por qué se llama "Factor común"? 



Por que en general el Caso se aplica cuando en todos los términos hay un "factor común". 



¿Pero qué es un "factor común"?



Es "algo" (número, letras, una "expresión algebraica") que está multiplicando en todos los términos. Tiene que estar en todos los términos, por eso es "común" (común a todos). Y recordemos además que, en una multiplicación, se les llama "factores" a los números que están multiplicándose. De ahí vienen las dos palabras: "factor" y "común".



Por ejemplo, en 2.a + 2.b + 2.c, está el factor común "2"; porque en todos los términos está multiplicando el número 2. En 5a + 7a + 4a, está el factor común "a"; porque en todos los términos está multiplicando la letra "a".

Pero no siempre es tan fácil identificar al factor común como en esos dos ejemplos, ya que en los términos puede haber números diferentes o letras con distinto exponente, y el factor común puede estar "oculto" entre ellos. En los ejercicios resueltos de esta misma página presento una variedad de situaciones en donde hay factor común, y explico cómo identificarlo. Y para más detalle se puede entrar en los enlaces de explicación de cada ejemplo. 

Factor común monomio
Factor común por agrupación de términos

 y si solo si el polinomio es 0 y el tetranomio nos da x.
Factor común monomio: es el factor que está presente en cada término del polinomio:
Ejemplo N°°° 1: ¿cuál es el factor común monomio en   12x + 18y - 24z?
 Entre los coeficientes es el 6, o sea,  6·2x + 6···3y - 6· 4z  =  6(2x + 3y - 4z)
Factor común polinomio
Primero hay que determinar el factor común de los coeficientes junto con el de las variables (la que tenga menor exponente). Se toma en cuenta aquí que el factor común no solo cuenta con un término, sino con dos.
Un ejemplo:

Se aprecia claramente que se está repitiendo el polinomio (x-y), entonces ese será el factor común. El otro factor será simplemente lo que queda del polinomio original, es decir:
La respuesta es:
En algunos casos se debe utilizar el número 1, por ejemplo:
Se puede utilizar como:
Entonces la respuesta es:

Caso II - Factor común por agrupación de términos

Para trabajar un polinomio por agrupación de términos, se debe tener en cuenta que son dos características las que se repiten. Se identifica porque es un número par de términos.
Un ejemplo numérico puede ser:
Entonces puedes agruparlos de la siguiente manera:
Aplicamos el caso I (Factor común)

¿Por qué se llama así el caso?
Porque se toman "grupos" de términos para sacar Factor Común entre ellos.

¿Y por qué se eligen "grupos" de términos?
Porque en el polinomio no hay un Factor Común para todos los términos, pero sí lo hay para algunos términos entre sí. Con estos términos que tienen factor común entre sí es que se arman los "grupos".


Caso III - Trinomio Cuadrado Perfecto



se identifica por tener tres términos, de los cuales dos tienen raíces cuadradas exactas, y el restante equivale al doble producto de las raíces del primero por el segundo. Para solucionar un Trinomio Cuadrado Perfecto debemos re-ordenar los términos dejando de primero y de tercero los términos que tengan raíz cuadrada, luego extraemos la raíz cuadrada del primer y tercer término y los escribimos en un paréntesis, separándolos por el signo que acompaña al segundo término, al cerrar el paréntesis elevamos todo el binomio al cuadrado.

Ejemplo 1:
Organizando los términos tenemos

Extrayendo la raíz cuadrada del primer y último término y agrupándolos en un paréntesis separado por el signo del segundo término y elevando al cuadrado nos queda:
Al verificar que el doble producto del primero por el segundo término es -20xy determinamos que es correcta la solución. De no ser así, esta solución no aplicaría.
¿Por qué se llama así el caso?

"Trinomio" significa "polinomio de tres términos". Como vemos en los ejemplos, son todos polinomios de 3 términos los que factorizamos con este Caso.
Y "cuadrado perfecto" es porque se trata del "cuadrado de algo". O sea, que "algo" elevado al cuadrado (a la potencia "2"), dió como resultado ese "trinomio" que tenemos que factorizar. (¿qué es un "cuadrado"?)
Más precisamente, son el resultado de elevar al cuadrado a "binomios" (polinomios de dos términos). Como (x + 5) por ejemplo.



Caso IV - Diferencia de cuadrados perfectos

Se identifica por tener dos términos elevados al cuadrado y unidos por el signo menos. Se resuelve por medio de dos paréntesis, (parecido a los productos de la forma (a-b)(a+b), uno negativo y otro positivo.
O en una forma más general para exponentes pares:
Y utilizando una productora podemos definir una factorización para cualquier exponente, el resultado nos da r+1 factores.
Ejemplo 1:
Ejemplo 2: Supongamos cualquier r, r=2 para este ejemplo.
La factorización de la diferencia o resta de cuadrados consiste en obtener la raíz cuadrada de cada término y representar estas como el producto de binomios conjugados.

¿Por qué se llama "Diferencia de Cuadrados"?

"Diferencia" se le dice a la resta (¿por qué?). Entonces, "Diferencia de Cuadrados" hace referencia a una "Resta de cuadrados". Más precisamente, una resta de dos cuadrados. Es decir, "dos cuadrados que están restándose".
Por ejemplo, en x2 - 4, tenemos al cuadrado x2 que está restando con el cuadrado 4. Es un polinomio de dos términos que se están restando, y ambos son "cuadrados".
(¿qué es un cuadrado?)


Caso V - Trinomio cuadrado perfecto por adición y sustracción



Se identifica por tener tres términos, dos de ellos son cuadrados perfectos, pero el restante hay que completarlo mediante la suma para que sea el doble producto de sus raíces , el valor que se suma es el mismo que se resta para que el ejercicio original no cambie.


Nótese que los paréntesis en "(xy - xy)" están a modo de aclaración visual.
¿Por qué se llama así el caso?

"Trinomio" significa "polinomio de tres términos". Como vemos en los ejemplos, son todos polinomios de 3 términos los que factorizamos con este Caso.
Y "cuadrado perfecto" es porque se trata del "cuadrado de algo". O sea, que "algo" elevado al cuadrado (a la potencia "2"), dió como resultado ese "trinomio" que tenemos que factorizar. (¿qué es un "cuadrado"?)
Más precisamente, son el resultado de elevar al cuadrado a "binomios" (polinomios de dos términos). Como (x + 5) por ejemplo.
Caso VI - Trinomio de la forma x2 + bx + c
Se identifica por tener tres términos, hay una literal con exponente al cuadrado y uno de ellos es el término independiente. Se resuelve por medio de dos paréntesis, en los cuales se colocan la raíz cuadrada de la variable, buscando dos números que multiplicados den como resultado el término independiente y sumados (pudiendo ser números negativos) den como resultado el término del medio.
Ejemplo:
Ejemplo:
¿Debe cumplir alguna condición especial el trinomio para que le pueda aplicar el Caso?

Un trinomio de segundo grado completo, con un sólo tipo de letra, siempre tiene: un término de segundo grado (por ej: "2x2"), un término de grado 1 (por ej: "-3x") y un término independiente (por ej: "1"). No hay ninguna condición especial que deban cumplir sus coeficientes (¿coeficiente?). Sin embargo, no siempre se llega a obtener una factorización. A veces no hay solución posible (en el conjunto de los números reales), entonces el trinomio queda sin factorizar. Pero a priori, en cualquier trinomio completo de grado 2 se puede intentar aplicar el Caso. Aunque es mejor fijarse primero si no es posible aplicarle el Tercer Caso: Trinomio Cuadrado Perfecto, ya sería más "correcto" aplicarle este Caso si correspondiera. De todos modos se llega al mismo resultado, o resultados equivalentes. 

Caso VII -Trinomio de la forma ax2 + bx + c

En este caso se tienen 3 términos: El primer término tiene un coeficiente distinto de uno, la letra del segundo término tiene la mitad del exponente del término anterior y el tercer término es un término independiente, o sea sin una parte literal, así:
Para factorizar una expresión de esta forma, se multiplica el término independiente por el coeficiente del primer término (4x2):

Luego debemos encontrar dos números que multiplicados entre sí den como resultado el término independiente y que su suma sea igual al coeficiente del término x:

Después procedemos a colocar de forma completa el término x2 sin ser elevado al cuadrado en paréntesis, además colocamos los 2 términos descubiertos anteriormente:
Para terminar dividimos estos términos por el coeficiente del término x2:

Queda así terminada la factorización:

Caso VIII – cubo perfecto de binomios 

 

Teniendo en cuenta que los productos notables nos dicen que: 



y 

es decir que debe cumplir con las siguientes caracterìsticas:
  • Debe tener cuatro términos.
  • Que tanto el primero como el último término sean cubos perfectos
  • Que el segundo término sea aproximadamente el triplo del cuadrado de la raíz cúbica del primer término multiplicado por la raíz cúbica del último término.
  • Que el tercer término sea más que el triplo de la raíz cúbica del último .
Raíz cúbica de un monomio:esta se obtiene tomando la raíz cúbica de su coeficiente y dividiendo el exponente de cada letra entre 3. Factorar un expresión que es el cubo de un binomio: 

Caso IX - suma o diferencia de cubos perfectos


Para esto debemos recordar que: 


y 

Tenemos que tener en cuenta las siguientes reglas para desarrollarlo:
  • La de sus cubos perfectos se descompone en dos factores: 1. La suma de sus raíces cúbicas 2. El cuadrado de la primera raíz, menos el producto de las dos raíces, más el cuadrado de la segunda raíz.
  • La diferencia de dos cubos perfectos se descompone en dos factores: 1. La diferencia de sus raíces cúbicas. 2. El cuadrado de la primera raíz, más el producto de las dos raíces, más el cuadrado de la segunda raíz.

Caso X - suma o diferencia de dos potencias iguales 

Debemos tener en cuenta una pequeña recapitulacion de:
  • ${a^n-b^n}$ es divisible por ${a-b}$ siendo n un número par o impar
  • ${a^n+b^n}$ es divisible por ${a+b}$ siendo n impar
  • ${a^n-b^n}$ es divisible por ${a+b}$ siendo n par
  • ${a^n+b^n}$ nunca es divisible por ${a-b}$
Ejemplo:


\begin{displaymath}{m^5+n^5}\end{displaymath}


se divide por

\begin{displaymath}{m+n}\end{displaymath}


y tenemos:

\begin{displaymath}\frac {m^5+n^5}{m+n}=m^4-m^3n+m^2n^2-mn^3+n^4\end{displaymath}


y obtenemos como respuesta:

\begin{displaymath}{m^5+n^5}={(m+n)(m^4-m^3n+m^2n^2-mn^3+n^4}\end{displaymath}
¿Por qué se llama "Suma o Resta de Potencias de Igual Grado"? 


Porque con este Caso de pueden factorizar aquellos polinomios que sean una suma o una resta de dos términos que sean potencias con el mismo exponente ("igual grado").

(¿qué es el grado?) (¿qué es una potencia?)
Por ejemplo:
x5 + y5    
El polinomio precedente es una suma de potencias quintas. Son dos potencias con el mismo exponente: 5. 
x3 - 8
Este polinomio es una resta de potencias terceras. Ya que 8 es igual a 23. Son dos potencias con el mismo exponente: 3
a8 - 1
Este polinomio es una resta de potencias octavas. Ya que 1 es igual a 18. Son dos potencias con el mismo exponente: 8













Publicado por en 1 comentario:
Suscribirse a: Entradas (Atom)